Cauchy

[3]:

# Parameters
func_name = "Cauchy"
positive_prior = False

Description

[5]:

func.display()

description: The Cauchy distribution
formula: $ K \frac{1}{ \gamma \pi} \left[ \frac{\gamma^2}{(x-x_0)^2 + \gamma^2} \right] $
parameters:
- K:
  - value: 1.0
  - desc: Integral between -inf and +inf. Fix this to 1 to obtain a Cauchy distribution
  - min_value: None
  - max_value: None
  - unit:
  - is_normalization: False
  - delta: 0.1
  - free: True
- x0:
  - value: 0.0
  - desc: Central value
  - min_value: None
  - max_value: None
  - unit:
  - is_normalization: False
  - delta: 0.1
  - free: True
- gamma:
  - value: 1.0
  - desc: standard deviation
  - min_value: 1e-12
  - max_value: None
  - unit:
  - is_normalization: False
  - delta: 0.1
  - free: True

Shape

The shape of the function.

If this is not a photon model but a prior or linear function then ignore the units as these docs are auto-generated

[6]:

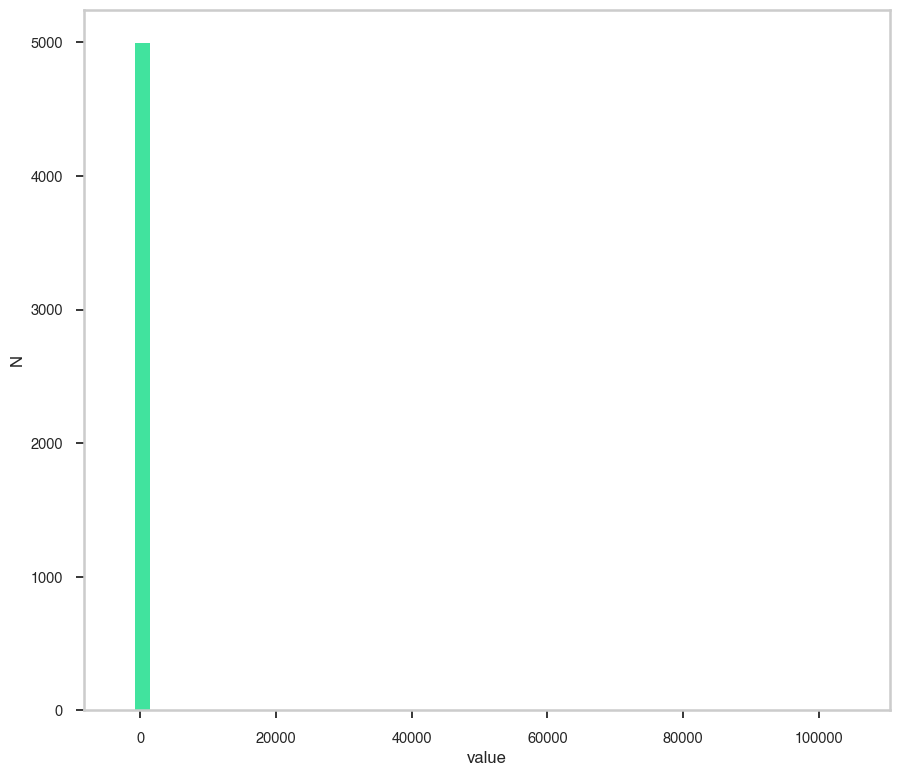
fig, ax = plt.subplots()

ax.plot(energy_grid, func(energy_grid), color=blue, lw=3)

ax.set_xlabel("x")
ax.set_ylabel("probability")

[6]:

Text(0, 0.5, 'probability')

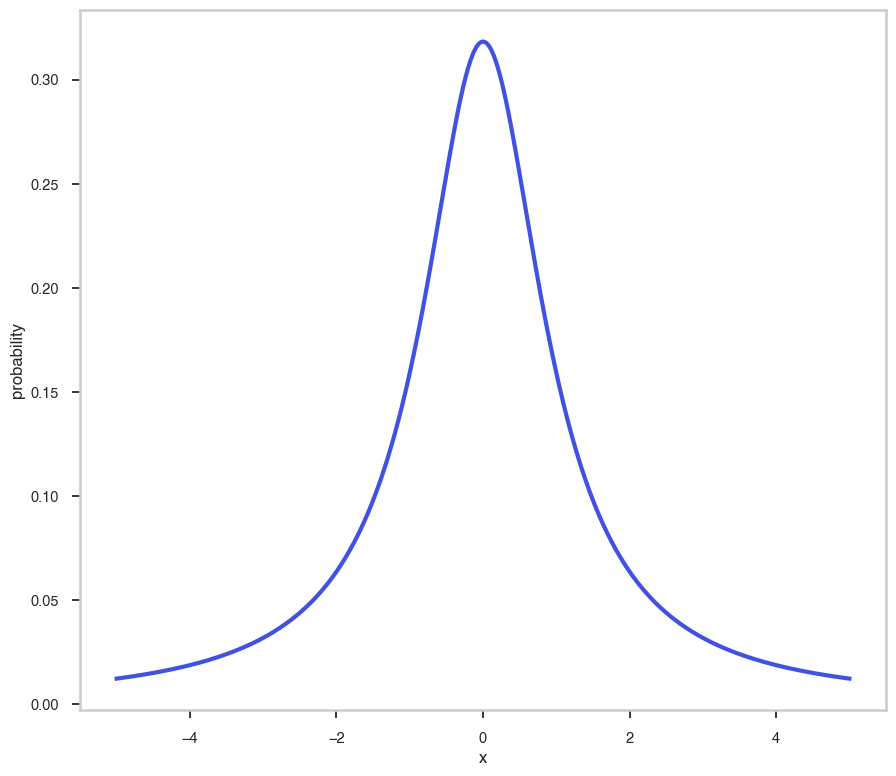
Random Number Generation

This is how we can generate random numbers from the prior.

[7]:

u = np.random.uniform(0,1, size=5000)

draws = [func.from_unit_cube(x) for x in u]

fig, ax = plt.subplots()

ax.hist(draws, color=green, bins=50)

ax.set_xlabel("value")
ax.set_ylabel("N")

[7]:

Text(0, 0.5, 'N')